重み付きマッチング概観 -

この記事は「数理最適化 Advent Calendar 2020」 $3$ 日目の記事です．*1
$2$ 日目は @taka_horibe さんによる「凸最適化の概要と主双対内点法のアルゴリズムの解説」です．
$4$ 日目は @kievdhia さんによる「確率計画法とその周辺の紹介」です．

今回は数理最適化ということで，線形計画と関連が深い組合せ最適化の話を書こうと思います．具体的には，グラフのマッチング問題に関する話を（技術的には深入りせずに）書きます．キーワードを散りばめておきますので，興味を持って深く知りたいという方は，ぜひ専門書 *2 を手に取って勉強してみてください．

線形計画に関連する部分では，線形計画に関する基礎知識を仮定します．また，グラフやマッチング等に関しては，一昨年のアドカレや昨年のアドカレの記事が参考になるかと思います．以下では，入力グラフの頂点数と枝数をそれぞれ $n$ と $m$ で表します．

問題設定

まず，重み付きマッチングと呼ばれる問題は，主に $2$ 種類あります． $1$ つは，枝重み付きグラフが与えられて，重み和が最大のマッチングを求めるという自然な設定です．もう $1$ つは，頂点数が偶数であるような枝重み付きグラフが与えられて，重み和が最小の完全マッチングを求めるという設定です．

最大重みマッチング問題 (Maximum Weight Matching)
入力 $G = (V, E)$ : グラフ， $w \colon E \to \mathbf{R}$ : 枝重み
目標 $w$ に関して重み和が最大であるような $G$ 中のマッチング $M$ の発見

最小重み完全マッチング問題 (Minimum Weight Perfect Matching)
入力 $G = (V, E)$ : グラフ $(n: 偶数)$ ， $w \colon E \to \mathbf{R}$ : 枝重み
目標 $w$ に関して重み和が最小であるような $G$ 中の完全マッチング $M$ の発見

後者は前者に比べると自然に見えないかもしれませんが，実は，入力を適切に変形することで相互に（多項式時間）帰着可能です．ちょうどいい演習問題なので，興味があれば考えてみてください．*3 そして，後者の方が何かと議論がしやすいので，以下では後者の問題に注目して話を進めていきます．

応用例

昨年のアドカレ記事にも出てきたように，重み付きマッチングに帰着することで，多項式時間で解けるという問題も色々あります．せっかくなので，その例に関して帰着を見てみましょう．

最短奇パス問題 (Shortest Odd Path)
入力 $G = (V, E)$ : 無向グラフ， $\ell \colon E \to \mathbf{R}_{\ge 0}$ : 枝長， $s, t \in V$ : 端点対
目標 $\ell$ に関して最短であるような $G$ 中の奇数枝数 $s$ – $t$ パス $P$ の発見

f:id:ygussany:20201201215637p:plain — 図 1: 最短奇パス問題での実行不能解 P' と最適解 P の例

f:id:ygussany:20201201215654p:plain — 図 1: 最短奇パス問題での実行不能解 P' と最適解 P の例

この問題を，最小重み完全マッチング問題に帰着しましょう．以下では，図 1 の具体例を用いて帰着方法を示します．

まず，最短奇パス問題の入力グラフを複製して $2$ つに増やし，同じ頂点由来の頂点同士を重み $0$ の枝で結びます（図 2 参照）．元のグラフ由来の枝の重みは，枝長をそのまま採用します．

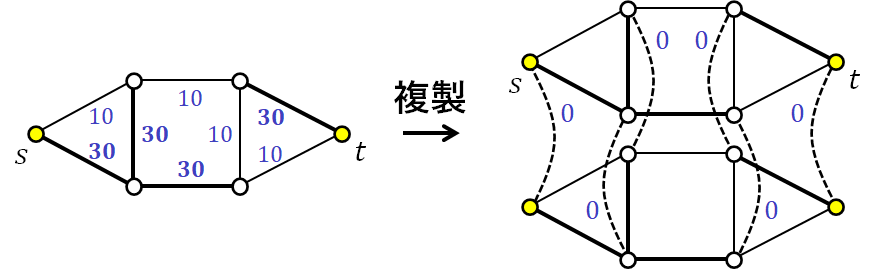
f:id:ygussany:20201201220451p:plain — 図 2: 入力グラフを複製

そして， $s$ と $t$ のコピーを，一方だけ接続枝もろとも除去します．その結果得られるグラフは， $s$ と $t$ だけがマッチされないような，重み和 $0$ の自明なマッチングを持ちます（図 3 参照）．

f:id:ygussany:20201201221148p:plain — 図 3: 帰着先のグラフにおける自明なマッチング

この自明なマッチングから，完全マッチングへの増加道（マッチされていない頂点同士を結び，マッチ枝と非マッチ枝を交互に通るようなパス）*4 を考えてみましょう．すると，増加道中の非マッチ枝は，元のグラフにおける $s$ – $t$ パスを構成し，その枝数は必ず奇数 *5 となります（図 4 参照）．逆に，元のグラフの奇 $s$ – $t$ パスは，帰着先での増加道に対応します．

f:id:ygussany:20201201221648p:plain — 図 4: 元グラフにおける奇パスと帰着先の増加道

したがって，帰着先のグラフの完全マッチングは，元のグラフの奇 $s$ – $t$ パスと概ね対応します．注意を要するのが，図 5 のように，奇 $s$ – $t$ パスといくつかの閉路に分かれる場合です．しかし，元の問題における枝長が非負であったことと，帰着先のグラフで最小重み完全マッチングを求めることを思い出すと，このような閉路は存在したとしても長さの総和が $0$ であるはず *6 なので，無視することができます．

f:id:ygussany:20201201222441p:plain — 図 5: 完全マッチングに対応する非負閉路の存在可能性

ということで，以上の手順で構成したグラフで最小重み完全マッチングを求めれば，元のグラフでの最短奇 $s$ – $t$ パスが求まるので，これにて帰着が完了となります．

マッチング多面体と線形計画緩和

では，重み付きマッチング問題をどうやって解けばよいでしょうか．最小重み完全マッチング問題を，整数線形計画問題として素朴に定式化すると，以下のようになります．

\begin{align}
\begin{array}{rll}
\mathrm{Minimize} & \displaystyle\sum_{e \in E} w_ex_e \\
\mathrm{subject~to} & \displaystyle\sum_{e \in \delta_G(v)} x_e = 1 & (v \in V)\\
& x_e \in \{0, 1\} & (e \in E)
\end{array}\tag{1}
\end{align}

ここで， $x_e$ は枝 $e$ をマッチングに含めるかどうかを表す変数で， $\delta_G(v)$ は $G$ 中で頂点 $v$ に接続する枝の集合を表します．すなわち，「各頂点周りで，ちょうど $1$ 本の枝を選んでください」というのが $2$ 行目の制約であり，これはまさしく完全マッチングとして要求される条件そのものです．また，目的関数は選んだ枝の重みの総和を表現しており，これを最小化せよと言っているので，最小重み完全マッチング問題を定式化できていることになります．

入力グラフが $2$ 部グラフである場合には， $x_e \in \{0, 1\}$ という整数制約を $x_e \ge 0$ という非負制約に緩和して得られる実行可能領域（多面体）が，完全マッチングの特性ベクトル *7 の凸包と一致することが知られています．*8 したがって， $(1)$ の線形計画緩和問題を考えて，その端点最適解を求めれば，最小重み完全マッチングが得られます．考えるべき線形計画問題では，変数が $m$ 個，制約が $n$ 個（と非負制約が $m$ 個）であり，これは元の入力グラフに関して多項式サイズなので， $2$ 部グラフの最小重み完全マッチングは多項式時間で求まることが分かります．*9

しかし，これは非 $2$ 部グラフでは必ずしも成り立ちません．具体的には，頂点数が奇数の閉路に関して，各枝に $\frac{1}{2}$ ずつ値を乗せても $2$ 行目の制約は（少なくとも部分的には）満たされていますが，そのような部分を完全マッチングの凸結合として表現することはできません．なぜなら，どのようなマッチングを持ってきても，頂点数が奇数 $k$ であるような誘導部分グラフ内では，枝を高々 $\frac{k - 1}{2}$ 本しか取れないのに対し，頂点数が $k$ の閉路の各枝に $\frac{1}{2}$ ずつ値を乗せると，その合計が $\frac{k}{2}$ となってしまうからです（図 6 参照）．

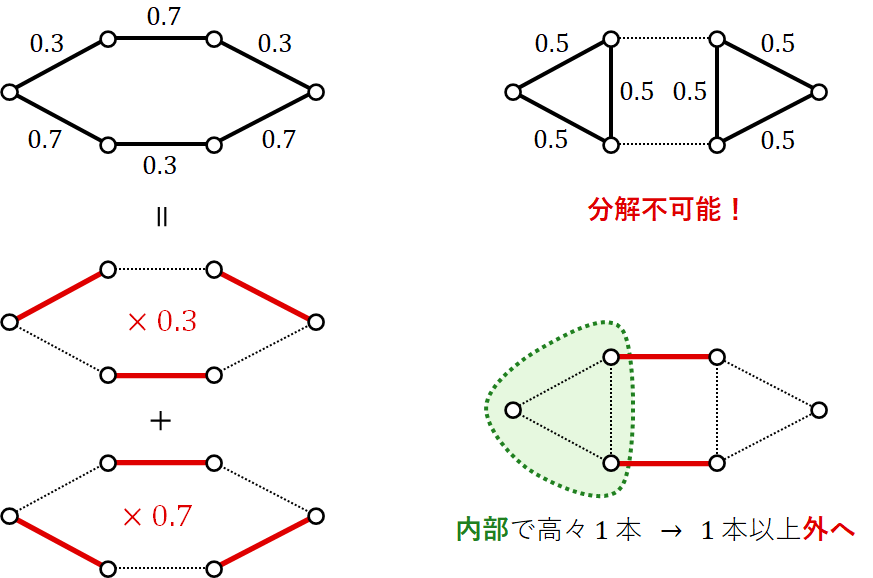
f:id:ygussany:20201201235529p:plain — 図 6: 完全マッチングの凸結合による表現可能性と追加制約 (2) の気持ち

そこで，上のような状況を回避するために，以下のような制約を追加してみます．

\begin{align}\displaystyle\sum_{e \in \delta_G(U)} x_e \ge 1 \quad (U \subseteq V,~|U|: 奇数)\tag{2}\end{align}

ここで， $\delta_G(U)$ は， $G$ 中で頂点部分集合 $U$ と補集合 $V \setminus U$ を結ぶ枝の集合を表します．すなわち，「頂点数が奇数である誘導部分グラフ内では枝を取り過ぎずに，ちゃんと外部の頂点とマッチするように枝を取ってください」ということを要請しています．これは，元の「完全マッチングを求めたい」という要求を一切強めておらず，したがって，整数線形計画問題の実行可能領域としては $(1)$ と全く同じままになります．しかし，少なくとも上で見た状況（奇閉路に $\frac{1}{2}$ ずつ乗せる）を排除できているので，線形計画緩和問題の実行可能領域としては追加前よりも狭まっています．*10

そして，なんと， $(1)$ に $(2)$ の不等式制約を追加した後に線形計画緩和して得られる実行可能領域（多面体）は，完全マッチングの特性ベクトルの凸包と一致することが知られています．というわけで，これにて一件落着，最小重み完全マッチング問題が解けることが分かりました．めでたし，めでたし．

とはいきません．世の中そんなに甘くはないのです．

何が問題かと言うと， $(2)$ の不等式はめちゃくちゃ多いです．具体的には， $U$ として奇数サイズの頂点部分集合をすべて（ほとんど）取ってこないといけないので，その数は実に $2^{n-1}$ ぐらいあります．これは元の入力に対して指数的に大きいので，そのような線形計画問題に定式化できたからといって，元の問題が多項式時間で解けるとは言えません．どうしたものかという感じですが，これには $2$ 通りの解決方法があります．

$1$ つ目は，上記の線形計画緩和問題を楕円体法を用いて解くことです．楕円体法による解法では，「ある線形不等式系の分離問題 *11 を繰り返し（多項式回）解くことで，その線形不等式系が表す多面体上の線形関数最適化ができる」ということが保証されます．実際，指数個ある $(2)$ の不等式系に関する分離問題は，最小奇カット問題と呼ばれる組合せ最適化問題に帰着され，これは Gomory–Hu 木と呼ばれる最小カット族の簡潔表現を用いることで多項式時間で解くことができます．*12 元の $(1)$ にある不等式は多項式個しかないので，そちらは別で地道にチェックすることにすれば，確かに分離問題が多項式時間で解けることになり，楕円体法を用いることで最小重み完全マッチング問題が多項式時間で解けることが分かります．

$2$ つ目は，線形計画問題の双対性と相補性を利用することです．煩雑になるのでここでは詳細を省略しますが，定義通りに線形計画緩和問題の双対を取ると，双対問題の変数は指数個になります．しかし，その大部分の値を $0$ に保ったまま，主問題の解（マッチング）と双対問題の疎な解を保持・更新していき，最終的に主問題と双対問題の目的関数値を一致させられる（すなわち，両者を最適解にできる）ことが，Edmonds のアルゴリズム *13 として知られています．もう少しだけ具体的に述べると，相補性条件を満たす（双対解に基づく被約重みが $0$ となる）ような枝のみからなるグラフで増加道を探索し，暫定マッチングのサイズを増やせるならば増やし，そうでなければ，マッチされていない頂点から到達可能な範囲で疎な双対解 *14 を適切に更新する，という操作を繰り返します．これにより，指数個ある双対変数のうち，多項式個しか参照しないようなアルゴリズムを設計でき，結果として多項式時間で動作するアルゴリズムが得られます．

最後に，第 $3$ の選択肢として，拡張定式化に関して触れておきます．上で作った多面体は確かに指数個の不等式によって表現されていましたが，「本当にそのような形でしか表現できないのか？」という疑問が浮かびます．拡張定式化では，考える空間の次元を一旦上げて，高次元空間における多面体を適当な不等式系で表現し，元の空間に射影することで欲しい多面体を表現しようとします．全域木多面体など，上手くやれば不等式の数を指数個から多項式個に削減できることもあるのですが，残念ながらマッチング多面体に関しては， $2^{\Theta(n)}$ 個の不等式が必要であること *15 が近年示され，「シンプルに不等式の数を減らして何とかする」という方向の可能性は否定されたことになります．

まとめ

本稿では，重み付きマッチングに関する理論のほんの一部の概要と，応用例を $1$ つ紹介しました．基本的には線形計画緩和を通じて効率的なアルゴリズムが設計できる一方で，多面体表現自体が簡潔に書けるわけではない，というのは $1$ つの興味深いポイントかなと思います．応用に関しても，一見遠く離れていそうな問題が重み付きマッチングを通じて解けることもあり，なかなか強力な武器になるので，少しでも興味を持っていただけたなら嬉しいです．

*1:今年は何故か一年ぶりの更新とはなりませんでしたね．

*2:たとえば，以下の書籍がオススメで，この記事の内容の大部分はこちらに包含されています．
A. Schrijver: Combinatorial Optimization: Polyhedra and Efficiency, Springer, 2003. (ISBN: 9783540443896)

*3:ヒント: MWPM → MWM は，重みの正負を反転して，適当にかさ上げするとよいです．逆は，マッチされなかった頂点を救済するための頂点を適切に用意して，それらと元グラフの全頂点を適切な重みの枝で結ぶとよいです．決して，ちゃんと書く時間が足りなかったとか，面倒だったとかではありません．決して．

*4:このようなパスに沿ってマッチ枝と非マッチ枝を反転させると，サイズが $1$ 大きいマッチングが得られます．

*5:上下上下…上と通ることになるため．

*6:そうでなければ，元グラフで閉路ができないような（自明なマッチングの枝を使った）完全マッチングを取った方が，重み和が小さくなり矛盾．

*7:各枝をマッチングに含むか含まないかを $1/0$ で表した $E$ 次元ベクトル．

*8:いわゆる Birkhoff–von Neumann の定理というもので，「任意の二重確率行列は置換行列の凸結合で表せる」と言い換えることもできます．

*9:陽に線形計画緩和を経由せずとも， $2$ 部グラフの最小重み完全マッチング問題（通称割当問題）を効率的に解くアルゴリズムは様々あります．

*10:このように，緩和前の問題の実行可能領域を保ったまま，緩和後の問題の実行可能領域を削るような不等式を妥当不等式（あるいは切除平面）と呼びます．

*11:線形不等式系 $\mathcal{S}$ と，同じ空間内の点 $x$ を入力とし， $x$ が $\mathcal{S}$ の不等式をすべて満たしていれば Yes を，そうでなければ $\mathcal{S}$ で違反されている不等式を $1$ つ答える問題．

*12:M. W. Padberg and M. R. Rao: Odd minimum cut-sets and $b$ -matchings. Mathematics of Operations Research, 7 (1982), pp. 67–80. (DOI: 10.1287/moor.7.1.67)

*13:J. Edmonds: Paths, trees, and flowers. Canadian Journal of Mathematics, 17 (1965), pp. 449–467. (DOI: 10.4153/CJM-1965-045-4)

*14:重み無しマッチング問題に対する花縮約アルゴリズムを知っている人向けに補足すると，疎な双対解とは「縮約される花の層族への値の割当て」になります．

*15:T. Rothboss: The matching polytope has exponential extension complexity. Journal of the ACM, 64 (2017), pp. 1–19. (DOI: 10.1145/3127497)